Вакцинация от COVID-19: за и против

Мы не будем большими оригиналами, если скажем, что построение модели любого явления должно быть основано на проверенных, качественных и достоверных данных. Если мы говорим о вакцинации, то таких данных в свободном доступе нет, а получить значимую информацию хочется. Такая информация нужна для принятия решений. И вот преподаватели кафедры бизнес-информатики Антон Назаров, Дмитрий Назаров, Денис Ковтун решили исследовать эту проблему с точки зрения теории вероятностей, в частности, достаточно знаменитой теоремы Байеса. Заметим, что Байесовские рассуждения — формальный способ уточнить наши представления об окружающем мире, основываясь на наблюдаемых данных, и один из мощнейших методов интеллектуального анализа данных. Байесовская статистика очень хорошо согласуется с тем, как люди рассуждают в обычной жизни, делая выводы из имеющихся сведений. Сложность лишь в том, чтобы разбить этот процесс на шаги и привести к строгой математической форме. Для понимания логики рассуждений и для более глубокого изучения нам понадобится несколько обозначений:

P (дождь | наступила осень) = весьма высокая

Интерпретация этой записи весьма проста: «Вероятность дождя при условии, что наступила осень, очень высокая».

Итак, рассмотрим ситуацию с вакцинацией с точки зрения Байесовских рассуждений. Итак, достоверно известная информация о том, что вероятность тяжело заболеть при вакцинации для большинства людей очень низкая. Обратно, вероятность заболеть при отсутствии вакцины очень высокая. Запишем это в математической нотации:

P (не привитый человек | тяжело заболеть) = очень высокая

P (привитый человек | тяжело заболеть) = очень низкая.

То, что мы написали, понимают так: «насколько наши представления объясняют наблюдаемое явление». А что, если мы поменяем местами событие и условие. Что в этом случае произойдет и можно ли будет как-то оценить?

P (тяжело заболеть | привитый человек) –?

P (тяжело заболеть | не привитый человек) –?

А что означает эта запись с точки зрения обычной человеческой логики? По сути, необходимо определить, насколько хорошо то, что видит наблюдатель, согласуется с опытом. Другими словами, какова вероятность того, что наугад взятый привитый человек окажется тяжело заболевшим.

Начнем с предположений, которые, на наш взгляд, являются достаточно правдоподобными, а именно, что соотношение числа людей, вакцинировавшихся и тяжело заболевших к числу людей, не вакцинировавшихся и тяжело заболевших 2:8. Это вполне реальное предположение, было получено исходя из опроса ближайшего нашего (авторов статьи) окружения. То есть мы имеем следующее:

Со школы всем известно, что сумма противоположных вероятностей равна 1. Поэтому в нашем предположении:

Рассмотрим гипотетическую организацию численностью 800 человек, из них 200 человек привитых, а 80 человек болеют COVID-19.

Руководителю организации позвонили из Роспотребнадзора и сказали, что сотрудник его организации заболел COVID-19. Какова вероятность, что он не привит (привит). То есть нам необходимо найти вероятности событий, обозначенных ранее. Давайте интерпретируем нашу задачу графически (см. рис. 1) 

Рисунок 1. – Исходные данные задачи о ситуации по вакцинации и COVID-19

Красная фигура – число невакцинированных, синяя – вакцинированные, желтая – болеющие сотрудники организации. Желтая часть фигуры, находящаяся над синей фигурой, интерпретирует ситуацию привитый человек | тяжело заболеть. Желтая часть фигуры, находящаяся над красной фигурой, интерпретирует ситуацию непривитый человек | тяжело заболеть. Вероятности этой ситуации нами оценены выше. А вот обратные вероятности нам поможет оценить теорема Байеса (см. рис. 2), которая по априорной вероятности легко определяет апостериорную (условную вероятность).

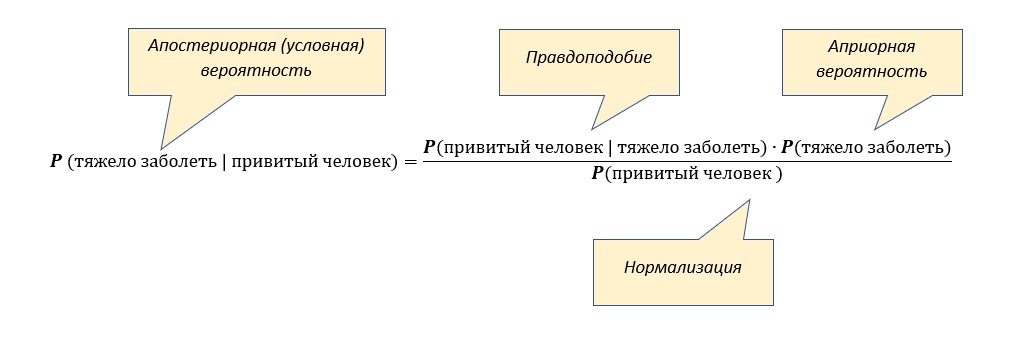
Рисунок 2. – Формула Байеса

Это означает, что тяжело заболеть при отсутствии вакцины в 1,5 раза вероятнее, чем при вакцинировании от COVID-19.

То, что мы построили, называется математическая модель. Все-таки, математика – это некоторое волшебство в руках профессионалов. Но мы живем в мире цифровой экономики и поэтому на основе этой модели можно построить имитационную, которая может достаточно точно предсказать совсем «неочевидные» для противников вакцинации вещи.

Будем строить имитационную модель в предположении, что около 10 человек в этой организации вакцинируются и примерно 20 инфицируются в неделю. При этом соотношение тяжело заболевших при вакцинации каждые 4 недели меняется на 1. Результаты работы модели показаны на рис. 3.

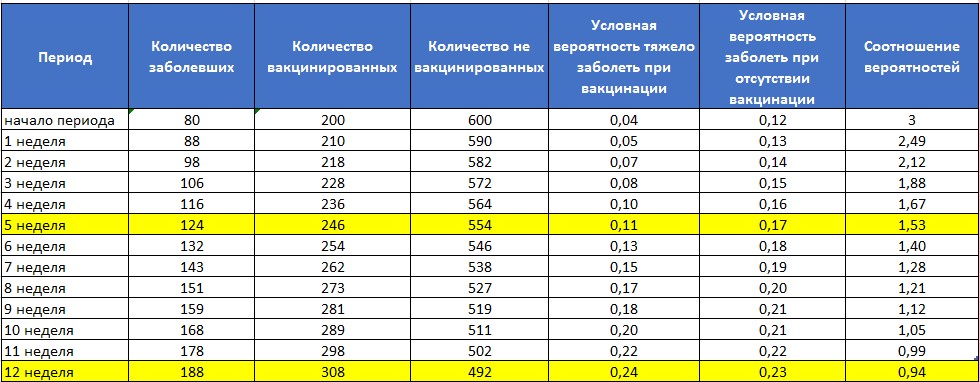
Рисунок 3. – Результаты процесса имитационного моделирования.

Что же показывает наша модель? Уже на исходе 5 недели вероятность того, что придет сообщение из Роспотребнадзора о заболевшем, снизится в 2 раза! А на конец 12 недели эти вероятности уравняются.

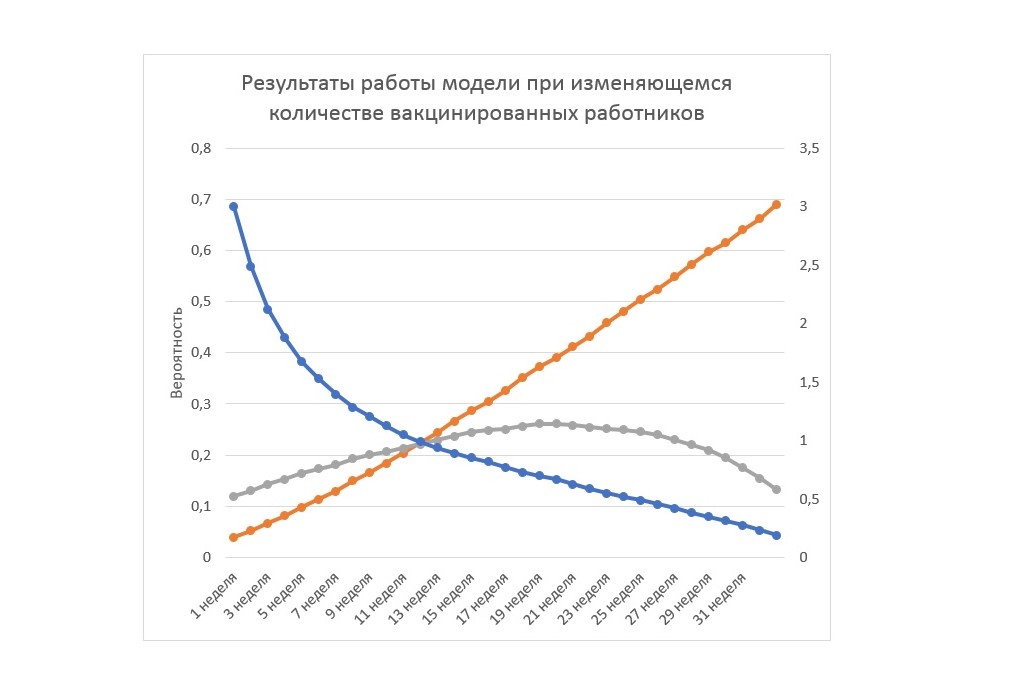
Рисунок 4. – Графические результаты имитационного моделирования

На графике видно, как меняются вероятности тяжело заболевших при вакцинации и при отсутствии вакцинации, а также их соотношение (по вспомогательной оси – справа). Известно, что эпидемиологический порог благоприятной ситуации наступает при 60%-80% вакцинированных. Анализируем данные рисунка 3 и видим, что такая ситуации при наших данных наступит уже на конец 30 недели, то есть фактически через 7 месяцев.

А если вакцинироваться будет большее число сотрудников, то такая ситуация наступит гораздо раньше! Мы провели такое исследование и получили, что при скорости вакцинации в примерно 20 сотрудников в неделю, уменьшается срок до 18 недель, 30 сотрудников – 11 недель.

Обеспечить безопасность на работе – в наших с вами силах. Вакцинируйтесь! 

Преподаватели кафедры бизнес-информатики провели анализ с точки зрения теории вероятностей.